Teorema de Pitágoras
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos . Es la proposición más conocida, entre otras, de las que tienen nombre propio en los contenidos de la matemática.
Si un triángulo rectángulo tiene catetos de longitudes  y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se formula que:
, se formula que:
 y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se formula que:
, se formula que:
De la ecuación () se deducen fácilmente tres corolarios de verificación algebraica y aplicación práctica:
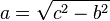

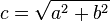
Historia
El teorema de Pitágoras tiene este nombre porque su demostración, sobre todo, es esfuerzo de la mística escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores
que se correspondían con los lados de un triángulo rectángulo, y se
utilizaban para resolver problemas referentes a los citados triángulos,
tal como se indica en algunas tablillas y papiros. Sin embargo, no ha perdurado ningún documento que exponga teóricamente su relación [cita requerida]. La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.
Designaciones convencionales

| Vértices |  |
 |
 |
| Lados (como segmento) |  |
 |
 |
| Lados (como longitud) |  |
 |
 |
| Ángulos |  |
 |
 |
Demostraciones
El teorema de Pitágoras es de los que cuenta con un mayor número de demostraciones diferentes, utilizando métodos muy diversos. Una de las causas de esto es que en la Edad Media se exigía una nueva demostración del teorema para alcanzar el grado de "Magíster matheseos".Algunos autores proponen hasta más de mil demostraciones. Otros autores, como el matemático estadounidense E. S. Loomis, catalogó 367 pruebas diferentes en su libro de 1927 The Pythagorean Proposition.
En ese mismo libro, Loomis clasificaría las demostraciones en cuatro grandes grupos: las algebraicas, donde se relacionan los lados y segmentos del triángulo; geométricas, en las que se realizan comparaciones de áreas; dinámicas a través de las propiedades de fuerza, masa; y las cuaterniónicas, mediante el uso de vectores.
China: el "Zhou Bi Suan Jing", y el "Jiu Zhang Suan Shu"
Prueba visual para un triángulo de a = 3, b = 4 y c = 5 como se ve en el Chou Pei Suan Ching, 500-200 a. C.
El "Zhou Bi" demuestra el teorema construyendo un cuadrado de lado (a+b) que se parte en cuatro triángulos de base a y altura b, y un cuadrado de lado c.
- Demostración
Sea el triángulo rectángulo de catetos a y b e hipotenusa c. Se trata de demostrar que el área del cuadrado de lado c es igual a la suma de las áreas de los cuadrados de lado a y lado b. Es decir:

Si añadimos tres triángulos iguales al original dentro del cuadrado de lado c
formando la figura mostrada en la imagen, obtenemos un cuadrado de
menor tamaño. Se puede observar que el cuadrado resultante tiene
efectivamente un lado de b - a. Luego, el área de este cuadrado menor puede expresarse de la siguiente manera:
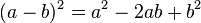
Es evidente que el área del cuadrado de lado c es la suma del área de los cuatro triángulos de altura a y base b que están dentro de él más el área del cuadrado menor:
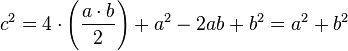
Demostraciones supuestas de Pitágoras
Se estima que se demostró el teorema mediante semejanza de triángulos: sus lados homólogos son proporcionales.3Sea el triángulo ABC, rectángulo en C. El segmento CH es la altura relativa a la hipotenusa, en la que determina los segmentos a’ y b’, proyecciones en ella de los catetos a y b, respectivamente.
Los triángulos rectángulos ABC, AHC y BHC tienen sus tres bases iguales: todos tienen dos bases en común, y los ángulos agudos son iguales bien por ser comunes, bien por tener sus lados perpendiculares. En consecuencia dichos triángulos son semejantes.

Demostración de Euclides: proposición I.47 de Los Elementos
El descubrimiento de los números irracionales por Pitágoras y los Pitagóricos supuso un contratiempo muy serio.6 De pronto, las proporciones dejaron de tener validez universal, no siempre podían aplicarse. La demostración de Pitágoras de su teorema se basaba muy probablemente en proporciones, y una proporción es un número racional. ¿Sería realmente válida como demostración? Ante esto, Euclides elabora una demostración nueva que elude la posibilidad de encontrarse con números irracionales.Demostración de Pappus
Unos 625 años después que Euclides, Pappus8 parece seguir su senda, y desarrolla una demostración del teorema de Pitágoras basada en la proposicón I.365 de Los Elementos de Euclides:- Dos paralelogramos de igual base, y entre las mismas paralelas, tienen superficies equivalentes.
Prolongando CH hacia arriba se obtiene el rectángulo CEGI cuya diagonal CG determina en aquél dos triángulos rectángulos iguales al triángulo ABC dado:
- Los ángulos agudos GCI y ABC tienen sus lados perpendiculares
- El lado CI es igual al lado CB
- Los paralelogramos ACGF y AHMN tienen la misma base CG=HM, y están comprendidos entre las mismas paralelas, r y s. Por lo tanto tienen la misma superficie (Elementos I.36)
- Aplicando el mismo principio a ACGF y ACED –base común AC, y paralelas m y n- resulta que ambos paralelogramos tienen superficies asimismo equivalentes.
Análogamente:
- CGJB y BLMH tienen la misma base CG=MH, y están comprendidos entre las paralelas s y t. Sus superficies son equivalentes.
- CGJB y CIKB tienen base común CB, y están entre las paralelas o y p. Sus superficies son iguales.
El teorema de Pitágoras queda demostrado.

Demostración de Bhaskara
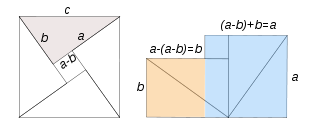
Bhaskara II, el matemático y astrónomo hindú del siglo XII, dio la siguiente demostración del teorema de Pitágoras.Con cuatro triángulos rectángulos de lados a, b y c se construye el cuadrado de lado c –izquierda-, en cuyo centro se forma otro cuadrado de lado (a-b).
Redistribuyendo los cuatro triángulos y el cuadrado de lado (a-b), construimos la figura de la derecha, cuya superficie resulta ser la suma de la de dos cuadrados: uno de lado a –azul- y otro de lado b -naranja-.
Demostración de Leonardo da Vinci
En el elenco de inteligencias que abordaron el teorema de Pitágoras no falta el genio del Renacimiento, Leonardo da Vinci.Partiendo del triángulo rectángulo ABC con los cuadrados de catetos e hipotenusa, Leonardo añade los triángulos ECF y HIJ, iguales al dado, resultando dos polígonos, cuyas superficies va a demostrar que son equivalentes:
- Polígono ADEFGB: la línea DG lo divide en dos mitades idénticas, ADGB y DEFG.
- Polígono ACBHIJ: la línea CI determina CBHI y CIJA.
- De inmediato vemos que tienen tres lados iguales: AD=AC, AB=AJ, BG=BC=IJ
- Asimismo es inmediata la igualdad entre los ángulos de los siguientes vértices:
- A de ADGB y A de CIJA
- B de ADGB y J de CIJA
De modo análogo se comprueba la igualdad entre ADGB y CBHI.
Además, de un modo semejante a lo explicado en la demostración de Euclides, nótese que un giro de centro A, y sentido positivo, transforma CIJA en ADGB. Mientras que un giro de centro B, y sentido negativo, transforma CBHI en ADGB.
Todo ello nos lleva a que los polígonos ADEFGB y ACBHIJ tienen áreas equivalentes. Pues bien, si a cada uno le quitamos sus dos triángulos –iguales- las superficies que restan forzosamente serán iguales. Y esas superficies no son sino los dos cuadrados de los catetos en el polígono ADEFGB, por una parte, y el cuadrado de la hipotenusa en el polígono ACBHIJ, por la otra. El teorema de Pitágoras queda demostrado.

Demostración de Garfield
James Abram Garfield (1831-1881), el vigésimo Presidente de los Estados Unidos,9 desarrolló una demostración del teorema de Pitágoras publicada en el New England Journal of Education.Garfield construye un trapecio de bases a y b, y altura (a+b), a partir del triángulo rectángulo de lados a, b y c. Dicho trapecio resulta compuesto por tres triángulos rectángulos: dos iguales al dado, y un tercero, isósceles de catetos c. En consecuencia:

Número irracional
En matemáticas, un número irracional es un número que no puede ser expresado como una fracción 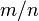 , donde
, donde  y
y  son enteros y
son enteros y  es diferente de cero. Es cualquier número real que no es racional. Un decimal infinito (id est con infinitas cifras) aperiódico, como
es diferente de cero. Es cualquier número real que no es racional. Un decimal infinito (id est con infinitas cifras) aperiódico, como
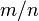 , donde
, donde  y
y  son enteros y
son enteros y  es diferente de cero. Es cualquier número real que no es racional. Un decimal infinito (id est con infinitas cifras) aperiódico, como
es diferente de cero. Es cualquier número real que no es racional. Un decimal infinito (id est con infinitas cifras) aperiódico, como
Historia
Dado que en la práctica de medir la longitud de un segmento de recta solo puede producir como resultado un número fraccionario, en un inicio, los griegos identificaron los números con las longitudes de los segmentos de recta.2 Al identificar del modo mencionado, surge la necesidad de considerar una clase de números más amplia que la de los números fraccionarios. Se atribuye a Pitágoras de Samos (580- 500a. C.) y su escuela el descubrimiento de la existencia de segmentos de recta inconmensurables con respecto a un segmento que se toma como unidad en un sistema de medición. Pues, existen segmentos de recta cuya longitud medida en este sistema no es un número fraccionario.3
Por ejemplo, en un cuadrado, la diagonal de este es inconmensurable con respecto a sus lados. Este hecho ocasionó una convulsión en el mundo científico antiguo. Provocó una ruptura entre la geometría y la aritmética de aquella época, ya que esta última, por entonces, se sustentaba en la teoría de la proporcionalidad, la cual solo se aplica a magnitudes conmensurables.
Intentaron salvar el obstáculo distinguiendo entre el concepto de número y el de longitud de un segmento de recta, y tomaron estos últimos como elementos básicos para sus cálculos. De tal modo, a los segmentos inconmensurables con respecto a la unidad tomada como patrón de medida les asignaron un nuevo tipo de magnitud: los números irracionales, los cuales por largo tiempo no se reconocieron como verdaderos números
Notación
No existe una notación universal para indicarlos, como , que es generalmente aceptada. Las razones son que el conjunto de Números Irracionales no constituyen alguna estructura algebraica, como sí lo son los naturales (
, que es generalmente aceptada. Las razones son que el conjunto de Números Irracionales no constituyen alguna estructura algebraica, como sí lo son los naturales ( ), los enteros (
), los enteros ( ), los racionales (
), los racionales ( ), los reales (
), los reales ( ) y los complejos (
) y los complejos ( ), por un lado, y que la
), por un lado, y que la  es tan apropiada para designar al conjunto de Números Irracionales como al conjunto de Números Imaginarios Puros, lo cual puede crear confusión. Fuera de ello,
es tan apropiada para designar al conjunto de Números Irracionales como al conjunto de Números Imaginarios Puros, lo cual puede crear confusión. Fuera de ello,
Clasificación
Tras distinguir los números componentes de la recta real en tres categorías (no excluyentes): (naturales, enteros y racionales), podría parecer que ha terminado la clasificación de los números, pero aún quedan "huecos" por rellenar en la recta de los números reales. Los números irracionales son los elementos de dicha recta que cubren los vacíos que dejan los números racionales. Debe notarse que aquí se está entendiendo como "recta real" el conjunto de las clases de equivalencia de sucesiones de Cauchy de números racionales. Puede demostrarse que el límite de algunas de esas sucesiones (de hecho la mayor parte de ellas), no es un número racional, por lo que si no se consideraran racionales existirían "huecos" en el conjunto de límites.
Los números irracionales son los elementos de la recta real que no pueden expresarse mediante el cociente de dos enteros y se caracterizan por poseer infinitas cifras decimales aperiódicas. De este modo, puede definirse al número irracional como una fracción decimal aperiódica infinita.5 En general, toda expresión en números decimales es solo una aproximación en números racionales al número irracional referido, por ejemplo, el número racional 1,4142135 es solo una aproximación a 7 cifras decimales del número irracional raíz cuadrada de 2, el cual posee infinitas cifras decimales no periódicas.
Entonces, decimos con toda propiedad que el número raíz cuadrada de dos es aproximadamente igual a 1,4142135 en 7 decimales, o bien es igual a 1,4142135… donde los tres puntos hacen referencia a los infinitos decimales que hacen falta y que jamás terminaríamos de escribir. Debido a ello, los números irracionales más conocidos son identificados mediante símbolos especiales; los tres principales son los siguientes:
 (Número "pi" 3,14159...): razón entre la longitud de una circunferencia y su diámetro.
(Número "pi" 3,14159...): razón entre la longitud de una circunferencia y su diámetro.- e (Número "e" 2,7182...):
 (Número "áureo" 1,6180...):
(Número "áureo" 1,6180...): 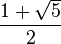
- las soluciones reales de x2 - 3 = 0; de x5 -7 = 0; de x3 = 11; 3x = 5; sen 7º, etc6
Los números irracionales se clasifican en dos tipos:
- Número algebraico: Son la solución de alguna ecuación algebraica y se representan por un número finito de radicales libres o anidados en algunos casos 7
; si "x" representa ese número, al eliminar radicales del segundo
miembro mediante operaciones inversas, queda una ecuación algebraica de
cierto grado. Todas las raíces no exactas de cualquier orden son
irracionales algebraicos. Por ejemplo, el número áureo es una de las raíces de la ecuación algebraica
 , por lo que es un número irracional algebraico.
, por lo que es un número irracional algebraico. - Número trascendente: No pueden representarse mediante un número finito de raíces libres o anidadas; provienen de las llamadas funciones trascendentes (trigonométricas, logarítmicas y exponenciales, etc.) También surgen al escribir números decimales no periódicos al azar o con un patrón que no lleva periodo definido, respectivamente, como los dos siguientes:
-
 ...
... ...
...
- Los llamados números trascendentes tienen especial relevancia ya que no pueden ser solución de ninguna ecuación algebraica. Los números pi y e son irracionales trascendentes, puesto que no pueden expresarse mediante radicales.
Propiedades
- La suma y la diferencia de un número racional y de un número irracional es un número irracional.
- El producto de un racional diferente de cero por un irracional es un número irracional.
- El cociente de un racional (≠ 0) entre un irracional es un número irracional.
- El inverso de un número irracional es número irracional.
- Sea un binomio, formado por un racional más un radical de segundo orden, o la suma de dos radicales de segundo orden, que es irracional. Entonces su conjugado es irracional.
- Los valores de logaritmos vulgares o naturales y los valores de las razones trigonométricas, la inmensa mayoría no numerable, son irracionales.
- El número de Gelfond (2 elevado a la raíz cuadrada de 2) es un número irracional trascendente8
- la raíz cuadrada de un número natural no cuadrado perfecto es un número irracional; también lo es la raíz enésima de un natural p que no es potencia enésima perfecta.
- Entre dos racionales distintos, existe por lo menos, un número irracional9
- Las razones trigonométricas de un ángulo son irracionales, excepcionalmente, una de ellas en el caso de que dos de los lados del triángulo rectángulo sean racionales.10
- La medida de Lebesgue de cualquier intervalo cerrado del tipo
![\scriptstyle[a,b]\cap\mathbb{I} \subset \R](https://upload.wikimedia.org/math/4/f/0/4f0dea00989786dd1fafcb21eba87c2e.png) es igual a la medida b-a.
Eso implica que si existiera un procedimiento para seleccionar al azar
un número de dicho intervalo, con probabilidad 1 el número obtenido
sería irracional.
es igual a la medida b-a.
Eso implica que si existiera un procedimiento para seleccionar al azar
un número de dicho intervalo, con probabilidad 1 el número obtenido
sería irracional. - Cualquier número irracional que está en un intervalo abierto de números reales es punto de acumulación de los números reales de tal intervalo, como de los números irracionales del mismo. Por ejemplo:
 es punto de acumulación de los números reales del intervalo
es punto de acumulación de los números reales del intervalo  , como también de los números irracionales de
, como también de los números irracionales de  . 11
. 11




no entendi una mierda
ResponderEliminarQue es esta mierda
ResponderEliminarSilencio maldito oscurantista
ResponderEliminarque puto
ResponderEliminarquedé mas colgado de lo que estaba, no entendí nada
ResponderEliminar